Lenguajes de alto nivel (Ejemplo de Cuadro Comparativo)

LENGUAJE	¿QUE ES?	VENTAJAS	DESVENTAJAS	SISTEMA OPERATIVO
C++	Lenguaje de programación orientada a objetos creado por Bjarne Stroustrup	Es potente en cuanto a lo que se refiere a creación de sistemas complejos un lenguaje muy robusto	No es atractivo visualmente No soporta para creación de páginas web	Sirve para todos los sistemas operativos pero cada uno con su respectiva versión para dicho sistema
HTML	Lenguaje utilizado para la creación de páginas web. HTML significa “hypertext mark-up language”, que significa, “lenguaje para el formato de documentos de hipertexto”, es decir, texto presentado de forma estructurada y agradable, con enlaces (hyperlinks) que conducen a otros documentos o fuentes	Sencillo que permite describir hipertexto. Archivos pequeños. Lenguaje de fácil aprendizaje. Lo admiten todos los exploradores	Lenguaje estático. La interpretación de cada navegador puede ser diferente. Guarda muchas etiquetas que pueden convertirse en “basura” y dificultan la corrección. Lento para ejecutar archivos pesados	Se pueden ver en todos los sistemas operativos, pero la interpretación varía según el navegador que esté utilizando.
VISUAL BASIC	Es un lenguaje de programación dirigido por eventos, desarrollado por el alemán Alan Cooper para Microsoft.	Posee una curva de aprendizaje muy rápida. Integra el diseño e implementación de formularios de Windows. Permite usar con facilidad la plataforma de los sistemas Windows, dado que tiene acceso prácticamente total al api de Windows, incluidas librerías actuales. Es uno de los lenguajes de uso más extendido, por lo que resulta fácil encontrar información, documentación y fuentes para los proyectos. Fácilmente extensible mediante librerías DLL y componentes ActiveX de otros lenguajes.	Las críticas hechas en las ediciones de visual Basic anteriores a vb.net son variadas,  se citan entre ellas:Problema de versionado asociado con varias librerías DLL, conocido como DLL HELL. Pobre soporte para programación orientada a objetos Incapacidad para crear aplicaciones multihilo, sin tener que recurrir a llamadas del api de Windows.	Sirve para hacer aplicaciones de escritorio
C#	Es un lenguaje de programación orientado. A objetos desarrollado y estandarizado por Microsoft como parte de su plataforma net. Los programadores le consideran el primo hermano de JAVA	Declaraciones en el espacio de nombres: al empezar a programar algo, se puede definir una o más clases dentro de un mismo espacio de nombres. Tipos de datos: en c# existe un rango más amplio y definido de tipos de datos que los que se encuentran en c, c++ o java. Atributos: cada miembro de una clase tiene un atributo de acceso del tipo público, protegido, interno, interno protegido y privado.	Se tiene que conseguir una versión reciente de visual studio .net, por otra parte se tiene que tener algunos requerimientos mínimos del sistema para poder trabajar adecuadamente tales como contar con Windows nt 4 o superior, tener alrededor de 4 gigas de espacio libre para la pura instalación, etc.	La plataforma .Net Sirve para hacer aplicaciones de escritorio, aplicaciones web y móviles. Sistema operativo Windows
XML	Es un estándar.Crea sus propias etiquetas permitiendo la definición, transmisión, validación e interpretación de datos entre aplicaciones y entre organizaciones. XML define datos portables al igual que java define código portable Lenguaje abierto, estándar derivado de SGML optimizando para su uso en la web	Permite la estructuración de la información Es la base de la nueva generación de aplicaciones web–intercambio de datos Poder etiquetar los datos con su significado Un lenguaje extendible	El mayor informe que las aplicaciones XML. Es que el navegador o el visualizador que el usuario utilice no cuente con un parcer capas de visualizar el contenido del documento	Todos los Sistemas Operativos
JAVA	Es un lenguaje orientado a objetos, de una plataforma independiente, fue desarrollado por la compañía SUN Microsystems ahora es propietario ORACLE. Maneja algunas plataformas de desarrollo: Java Platform, Standard Edition o Java SE Java Platform Enterprise Edition o Java EE Java Platform Micro Edition o Java ME	Se pueden realizar distintos aplicativos, como son applets, que son aplicaciones especiales, que se ejecutan dentro de un navegador al ser cargada una página HTML en un servidor web, por lo general los applets (Ya son historia) son programas pequeños y de propósitos específicos. Puede desarrollar  aplicaciones de escritorio que se ejecutan en forma independiente, es decir con la programación java, se pueden realizar aplicaciones como un procesador de palabras, una hoja que sirva para cálculos, una aplicación gráfica, etc. Se puede realizar soluciones empresariales en un entorno web Soporta el desarrollo de aplicaciones móviles	Esperar la actualización siguiente para que sea más rápido.	Sirve para todos los sistemas operativos y si no es la versión adecuada para dicho sistema, la misma aplicación java se encarga de descargas o actualizar versión para un excelente desempeño en el pc. Algunos de los sistemas operativos más destacados en los que funciona la aplicación: Unix, Linux, Solaris, Windows, mac.
PHP	PHP es un lenguaje de programación interpretado, diseñado originalmente para la creación de páginas web dinámicas	Es un lenguaje multiplataforma. Orientado al desarrollo de aplicaciones web dinámicas con acceso a información almacenada en una base de datos.	Como es un lenguaje que se interpreta en ejecución, para ciertos usos puede resultar un inconveniente que el código fuente no pueda ser ocultado. La ofuscación es una técnica que puede dificultar la lectura del código pero no la impide y, en ciertos casos, representa un costo en tiempos de ejecución.	Se usa principalmente para la interpretación del lado del servidor, páginas web y CMS Se usa en todos los sistemas operativos

Conectores logicos

  

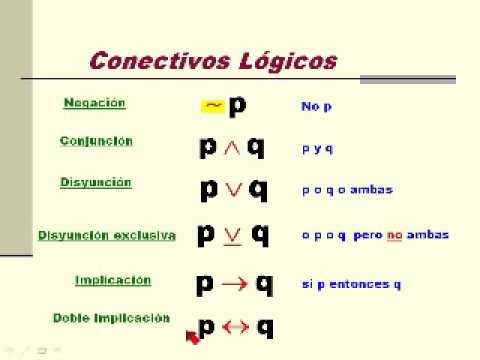
Los conectores lógicos son palabras o expresiones que sirven para relacionar las ideas dentro de un texto. En ese sentido, su presencia es fundamental para que un texto sea mucho más que un conjunto de oraciones independientes y autónomas. La claridad de la argumentación de un texto depende principalmente del uso adecuado de los conectores; un conector lógico mal utilizado puede cambiar completamente el sentido del texto.

Los conectores que utilizamos son:

• Negación (¬): El valor de verdad de la negación es el contrario de la proposición negada.

• La conjunción ( ∧) sirve para indicar que se cumplen dos condiciones simultáneamente, por ejemplo:

• Disyunción (v): La disyunción solamente es falsa si lo son sus dos componentes.

• Condicional (→): El condicional solamente es falso cuando el antecedente es verdadero y el consecuente es falso. De la verdad no se puede seguir la falsedad.
• Bicondicional (<--->):El bicondicional solamente es cierto si sus componentes tienen el mismo valor de verdad.

Tabla de la Verdad

.

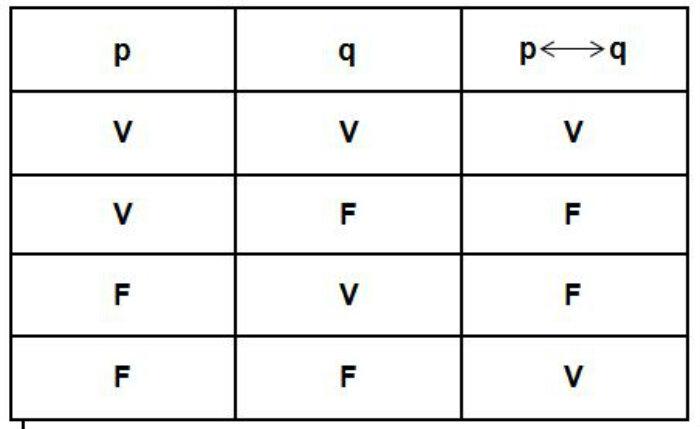
Tablas de verdad o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes.Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.Las tablas de verdad son, por una parte, uno de los métodos más sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma.

Construcción de Tablas de Verdad

Algoritmo para construir una tabla de verdad de una fórmula en lógica de proposiciones.

1. Escribir la fórmula con un número arriba de cada operador que indique su jerarquía. Se escriben los enteros positivos en orden, donde el número 1 corresponde al operador de mayor jerarquía. Cuando dos operadores tengan la misma jerarquía, se le asigna el número menor al de la izquierda.
2. Construir el árbol sintáctico empezando con la fórmula en la raíz y utilizando en cada caso el operador de menor jerarquía. O sea, del número mayor al menor.
3. Numerar las ramas del árbol en forma secuencial empezando por las hojas hacia la raíz, con la única condición de que una rama se puede numerar hasta que estén numerados los hijos. Para empezar con la numeración de las hojas es buena idea hacerlo en orden alfabético, así todos obtienen los renglones de la tabla en el mismo orden para poder comparar resultados.
4. Escribir los encabezados de la tabla las fórmulas siguiendo la numeración que se le dió a las ramas en el árbol sintáctico.
5. Asignarle a los átomos, las hojas del árbol, todos los posibles valores de verdad de acuerdo al orden establecido. Por supuesto que el orden es arbitrario, pero como el número de permutaciones es n!, conviene establecer un orden para poder comparar resultados fácilmente.
6. Asignar valor de verdad a cada una de las columnas restantes de acuerdo al operador indicado en el árbol sintáctico utilizando la tabla de verdad. Conviene aprenderse de memoria las tablas de los operadores, al principio pueden tener un resumen con todas las tablas mientras se memorizan.
7. La última columna, correspondiente a la fórmula original, es la que indica los valores de verdad posibles de la fórmula para cada caso.

Investigación #1

Investigación #1

1.¿Qué es una tabla de la verdad lógica o tabla de valores de verdad?
   R. Tabla de valores de verdad, es una tabla que despliega el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes.

2.¿Qué son las reglas de la verdad de informática lógica?
   R. Son los que nos ayudan a establecer el valor de verdad de diferentes razonamientos lógicos construidos a base de la combinación de 2 o más enunciados nucleares.

3.¿Qué es variable?
   R. Es un espacio en la memoria reservada para almacenar un valor determinado que corresponde a un tipo de dato por el lenguaje de programación en el cual se trabaja.

4.¿Qué es el valor verdadero?
   R. Es un valor que indica en qué medida una declaración es verdad.

5.¿Qué es el valor falso?
   R. El valor falso de una proposición es verdadera cuando dicha proposición es falsa y viceversa.

6.¿Qué es conjunción?
   R. Conector lógico cuyo valor de la verdad resulta en cierto sólo si ambas proposiciones son ciertas, y en falso de cualquier otra forma.​

7.¿Qué es disyunción?
   R. conector lógico, cuyo valor de la verdad resulta en falso sólo si ambas proposiciones son falsas, y en cierto de cualquier otra forma.​ 

8.¿Qué es implicación condicional?
   R. Es una instrucción o grupo de instrucciones que se puede o no ejecutar en función del valor de una condición.

9.¿Qué es equivalencia?
   R. Es una unidad de medida en informática y su símbolo es TB y es quivalente a 240 bytes.

10.¿Qué son los número de combinación de una variable?
   R. Es una rama de las matemáticas que estudia numeración.

11.¿Que significa una y dos variables?
   R. Está sujeta a cambios frecuentes o probables.

Glosario 1 (Rubén González)

1- Variable: son espacios reservados en la memoria que, como su nombre indica, pueden cambiar de contenido a lo largo de la ejecución  de un programa.

2- Conjunción: en lógica y matemáticas, es un operador lógico que resulta en verdadero si los dos operadores son verdaderos, de lo contrario si uno de los dos es falso, todo será falso.

3- Disyunción: es un operador lógico que resulta ser verdadero si cualquiera de los operadores es también verídico.

4- Implicación condicional: se refiere al hecho de que hay algo plegado o doblado en el interior de algo que oculta lo que hay en su interior.

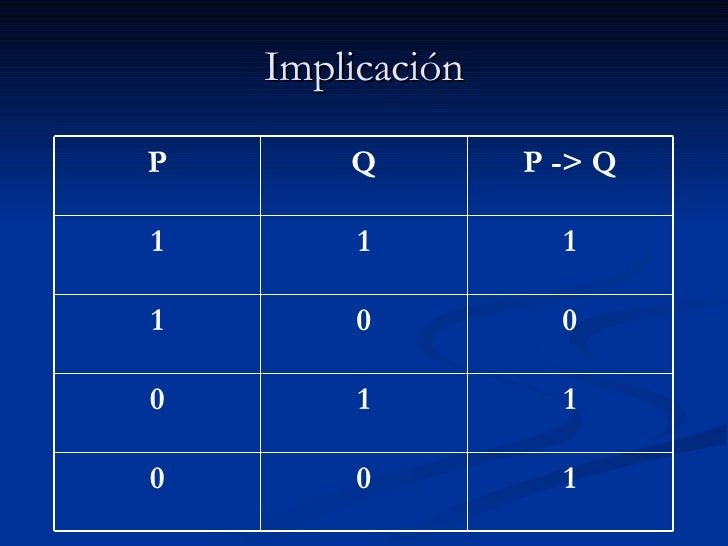5- Equivalencia: es verdadero cuando ambas proposiciones tienen el mismo valor de verdad es decir, ambas son verdaderas o falsas simultaneamente; de lo contrario es falso.
6- Lógica: método o razonamiento en el que ideas o la sucesión de los hechos se manifiestan o se desarrollan de forma coherente y sin que haya contradicciones entre ellas.
7- Algoritmo: conjunto ordenado de operaciones sistemáticas que permite hacer un cálculo y hallar la solución de un tipo de problemas.
8- Técnicas: es el conjunto de procedimientos, reglas, normas o protocolos que tiene como objetivo obtener un resultado determinado y efectivo, ya sea en el campo de la informática, las ciencias, el arte, el deporte, la educación o en cualquier otra actividad
9- Programación: es un proceso por el cual se escribe, se prueba, se depura y se mantiene el código fuente de un programa informático.
10- Datos: son la representación simbólica, bien sea mediante números o letras de una recopilación de información.

Cuadro comparativo de los lenguajes de programación (Victor García)

Pasos para el desarrollo lógico aritmético en la informática (Rubén González)

En computación, la unidad aritmética lógica o unidad aritmético-lógica, también conocida como ALU, es un circuitppo digital que calcula operaciones aritméticas (como suma, resta, multiplicación, etc.) y operaciones lógicas (si, y, o, no), entre valores (generalmente uno o dos) de los argumentos.

Una ALU debe procesar números usando el mismo formato que el resto del circuito digital. Para los procesadores modernos, este formato casi siempre es la representación del número binario de complemento a dos. Las primeras computadoras usaron una amplia variedad de sistemas de numeración, incluyendo complemento a uno, formato signo-magnitud, e incluso verdaderos sistemas decimales, con diez tubos por dígito.

Las ALU para cada uno de estos sistemas numéricos mostraban diferentes diseños, y esto influenció la preferencia actual por el complemento a dos, debido a que ésta es la representación más simple, para el circuito electrónico de la ALU, para calcular adiciones, sustracciones, etc.

PASOS PARA PLANTEAR LA SOLUCIÓN A UN PROBLEMA:

1.- Análisis del problema.

2.- Identificar las entradas, procesos y salidas del problema, declaración de variables.

3.- Diseño del Algoritmo: Describe la secuencia ordenada de los pasos, sin ambigüedad, es decir, siendo preciso y veraz en la búsqueda de la solución al problema.

4.- Codificación del Algoritmo: Es la expresión en un lenguaje de programación de los pasos definidos en el algoritmo.

5.- Ejecución y validación del programa por el computador.

Teoría para el desarrollo Lógico de problemas de algoritmo (Rubén González)

Razonamiento lógico

Es  la base para elaborar soluciones informáticas, tanto en software como en hardware. Es bien conocido que los profesionales que aplican adecuadamente el razonamiento lógico tiene mayores posibilidades de éxito, tanto en lo profesional como en lo personal, ya que analizar, saber buscar posibilidades, demostrar o refutar afirmaciones diversas, le permite a quien tiene ese conocimiento y manejo ser un mejor ser humano y por consiguiente un profesional con mayores y mejores aptitudes y actitudes para vivir en una sociedad como la actual, necesitada de ecuanimidad, raciocinio y capacidad de análisis para solucionar sus cada vez más complejos problemas.

Diseñar, desarrollar y mantener software son procesos netamente creativos que se sustentan fundamentalmente en la capacidad de razonamiento, en el pensamiento computacional y algorítmico y en la habilidad para abstraer cualquier problema, por lo que es necesario estructurar este curso para ofrecer una base sólida de la lógica en la línea computacional para los futuros ingenieros de sistemas. Desde la publicación de los trabajos de Herbrand en 1930 la lógica se ha convertido en un valioso instrumento conceptual al servicio de las ciencias computacionales, en la que ayudan para representar el conocimiento y para soportar el diseño de sistemas de información, es decir, hoy la lógica computacional se aborda desde la perspectiva de aplicación a la computación.

La principal razón para que las personas aprendan lenguajes de 
programación es utilizar un ordenador como una herramienta para la 
resolución de problemas. Tres fases pueden ser identificadas en el proceso 
de resolución : 

• - Fase de Identificación (qué nos plantean) 
• - Fase de resolución del problema 
• - Fase de implementación (realización) en un lenguaje de 
• programación

Sistema informático (Victor García)

Definición de Sistema informático  

No todos los sistemas de información son sistemas informáticos, pero todos los sistemas informáticos son sistemas de información. Por lo tanto se puede decir que un sistema informático es un subconjunto de un sistema de información.

Por ejemplo, el sistema de información de una biblioteca antiguamente se hacía manualmente: el ingreso de nuevos libros, las fichas de cada libro se llenaban a mano, las búsquedas de libros, la organización de los mismos en estantes, etc.

Con la llegada de la computadoras una biblioteca sigue contando con un sistema de información para organizarse, pero que a su vez contiene un sistema informático: una o más computadoras para buscar libros, para ingresarlos al sistema, para saber dónde están ubicados exactamente, un operador que controla las computadoras (el operador humano se considera parte parte del sistema), disponibilidad de impresoras, escáneres, manuales de uso del sistema, técnicos de mantenimiento del sistema, usuarios del sistema,  etc.

Un sistema informático es un conjunto de partes o recursos formados por el hardware, software y las personas que lo emplean, que se relacionan entre sí para almacenar y procesar información con un objetivo en común.

Son ejemplos de sistemas informáticos: sistema gestor de una biblioteca, un sistema de contabilidad computarizado, sistema de control de compras y ventas en una empresa.


Recursos de un Sistema Informático

Recurso físico (o de hardware): computadoras, impresoras, escáneres, memorias, lectores de código de barras, estructura física de una red de computadoras, etc.


Recurso lógico (o de software): manuales de uso, sistema operativo, archivos, documentos, aplicaciones, firmware, bases de datos, información de una red de computadoras, etc.


Recurso humano: son todos las personas que forman parte del sistema, como ser los operadores del sistema, los técnicos que lo mantienen y los usuarios finales.

variable lógica y combinada (Rubén González)

Variable Lógica

Símbolo que, en una fórmula lógica, indica de forma indeterminada los miembros de una clase y puede ser sustituido por cualquiera de ellos, por lo que se denominan valores de la variable.

Son aquellas que solo pueden tener dos valores (cierto o falso) estos representan el resultado de una comparación entre otros datos.

Variable combinada

describe una situación donde una variable depende de dos (o más) otras variables, y varía directamente con algunas de ellas y varia inversamente con otras (cuando el resto de las variables se mantuvieron constantes). 

Regla de la tabla de la verdad (Victor García)

Qué son las tablas de la verdad

Las tablas de verdad son, por una parte, uno de los métodos más sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma.

Estas tablas pueden construirse haciendo una interpretación de los signos lógicos como: no, o, y, si…entonces, sí y sólo si. La interpretación corresponde al sentido que estas operaciones tienen dentro del razonamiento. Puede establecerse una correspondencia entre los resultados de estas tablas y la deducción lógico matemática. En consecuencia, las tablas de verdad constituyen un método de decisión para chequear si una proposición es o no un teorema. Para la construcción de la tabla se asignará el valor 1(uno) a una proposición cierta y 0 (cero) a una proposición falsa.

Negación: El valor de verdad de la negación es el contrario de la proposición negada.
La conjunción sirve para indicar que se cumplen dos condiciones simultáneamente, por ejemplo:
La función es creciente y está definida para los números positivos, utilizamos Para que la conjunción p^q sea verdadera las dos expresiones que intervienen deben ser verdaderas y sólo en ese caso como se indica por su tabla de verdad.

Disyunción: La disyunción solamente es falsa si lo son sus dos componentes.
Con la disyunción a diferencia de la conjunción, se representan dos expresiones que afirman que una de las dos es verdadera, por lo que basta con que una de ellas sea verdadera para que la expresión p ∨ q sea verdadera.

Condicional: El condicional solamente es falso cuando el antecedente es verdadero y el consecuente es falso. De la verdad no se puede seguir la  falsedad.

Bicondicional:El bicondicional solamente es cierto si sus componentes tienen el mismo valor de verdad.

Otras tablas de verdad divergentes

Además de las tablas polivalentes e intencionales, hay muchas otras tablas de verdad. Por ejemplo, hay tablas de verdad en las que los renglones se bifurcan en dos o más sub-renglones y son útiles para lo que en lógica llamamos super-valuaciones. También existen tablas con valores y más de 2n renglones, ¿cómo es posible? Pues porque, a diferencia de las tablas tradicionales, en estas tablas el orden de los renglones sí importa, de tal manera que renglones repetidos cuentan como renglones distintos. Finalmente, también existen las tablas bidimensionales, usadas originalmente en ciertas lógicas intencionales, pero popularizadas gracias al trabajo de Robert Stalnaker y otros .

Tipos de lenguajes de programación (Victor García)

CONOCE LOS TIPOS DE LENGUAJES DE PROGRAMACIÓN: BAJO Y ALTO NIVEL 

Anteriormente, cuando solo existían los lenguajes de bajo nivel (código máquina y ensamblador), darle instrucciones al computador era una tarea bastante compleja y que requería mucho tiempo.

No sería hasta la llegada de Fortran (el primer lenguaje de alto nivel), en que ya no era necesario escribir en binario para darle instrucciones al ordenador.

Aquí te contamos todo lo que tienes que saber sobre estos lenguajes de alto nivel (compilador e interpretados) y bajo nivel (máquina y ensambl ador).

Un lenguaje de programación es, básicamente, el medio para darle instrucciones al computador.

Los ordenadores tienen millones de interruptores que están encendidos (1) o bien apagados (0). Así, puedes darle instrucciones al ordenador por medio de bits (cadenas de 0s y 1s). Sin embargo, esto resulta demasiado complejo.

Es por ello que se crearon los lenguajes de programación de alto nivel, para escribir código legible que será traducido al lenguaje máquina (binario). Es decir, para que sean intermediarios entre los desarrolladores y el hardware.

Lenguajes de programación de bajo nivel

Los lenguajes de bajo nivel son aquellos que están más próximos al lenguaje de máquina (de ceros y unos). Es decir, tienen un control directo sobre el hardware.

A diferencia de los lenguajes de alto nivel, no necesitan compiladores. Se ejecutan directamente en el procesador y dependen de la arquitectura del hardware.

Los programas que se crean con estos lenguajes de bajo nivel dependen totalmente del hardware. Por esta razón, no se pueden migrar o utilizar en otras máquinas.

Además, pese a que aprovechan mejor las características del hardware, son los tipos de lenguajes más difíciles de entender y aprender.

Existen dos tipos de lenguajes de bajo nivel: máquina y ensamblador.

a. Lenguaje de máquina
El lenguaje de máquina es aquel que es interpretado directamente por el procesador, por lo que su ejecución es mucho más rápida.

Así mismo, consta de cadenas de números binarios (0s y 1s). Por esta razón, programar en este lenguaje es una tarea difícil que requiere una gran inversión de tiempo.

Lenguaje de máquina

Cabe destacar que los programas escritos en este lenguaje no necesitan ser traducidos, pues es el único lenguaje que el procesador entiende directamente.

Además, pese a que hace un uso eficiente de la memoria, encontrar un fallo en el lenguaje de máquina es una tarea casi imposible.

b. Lenguaje ensamblador
El lenguaje ensamblador (assembler o asm) no es más que códigos mnemotécnicos (abreviaturas de letras y números) de las instrucciones máquina (binario).

En consecuencia, los programas escritos en ensamblador se traducen a código máquina de forma inmediata.

Lenguaje ensamblador

Lenguaje ensamblador – Imagen: Android Authority

Por otro lado, este lenguaje de bajo nivel depende estrictamente del tipo de procesador utilizado. Es por ello que programar en ensamblador requiere conocer, en forma detallada, las especificaciones del hardware.

De igual manera, el software escrito en este lenguaje resulta ser poco o nada portable. Aunque, como ventaja, ocupa menos memoria, es más fácil de depurar y su código fuente resulta más corto.

Lenguajes de programación de alto nivel

Los lenguajes de alto nivel están más próximos al lenguaje humano y más alejados de la máquina. Por lo tanto, resultan más fáciles de entender y son más flexibles a la hora de programar.

Además, este tipo de lenguaje de programación es traducido al lenguaje máquina mediante un intérprete o compilador.

Así mismo, al ser independientes del hardware, los programas escritos en estos lenguajes de alto nivel pueden ejecutarse en diferentes plataformas (Windows, Linux, etc.)

Por otro lado, al existir una gran cantidad de lenguajes de alto nivel, su clasificación es muy diversa.

Sin embargo, aquí vamos a señalar dos tipos de lenguajes de alto nivel: lenguajes compilados e interpretados.

a. Lenguajes compilados

Los lenguajes compilados son aquellos que son traducidos al lenguaje de máquina (cadenas de bits) de una sola vez.

En consecuencia, cada modificación que realices en el código fuente requiere volver a compilar (traducir a código máquina) todo.

Sin embargo, hay algunos lenguajes como Java que primero compilan a bytecode  (un código intermedio) y luego es interpretado a máquina.

Pensamiento Lógico Matemático (Rubén González)

Pensamiento lógico matemático

El razonamiento lógico matemátco no existe por si mismo en la realidad.La raíz del razonamiento lógico-matemático está en la persona.

 Cada sujeto lo construye por abstracción reflexiva. Esta abstracción reflexiva nade de la coordinación de las acciones que realiza el sujeto con los objetos.
El conocimiento lógico-matemático lo construye el niño al relacionar las experiencias obtenidas en la manipulación de los objetos. Un ejemplo más utilizado es que el niño diferencia entre un objeto de textura suave de otro de textura áspera.

LA IMPORTANCIA DEL PENSAMIENTO MATEMATICO

 El pensamiento Lógico-Matemático está relacionado con la habilidad de trabajar y pensar en términos de números y la capacidad de emplear el razonamiento lógico. El desarrollo de este pensamiento, es clave para el desarrollo de la inteligencia matemática y es fundamental para el bienestar de los niños y niñas y su desarrollo, ya que este tipo de inteligencia va mucho más allá de las capacidades numéricas, aporta importantes beneficios como la capacidad de entender conceptos y establecer relaciones basadas en la lógica de forma esquemática y técnica. Implica la capacidad de utilizar de manera casi natural el cálculo, las cuantificaciones, proposiciones o hipótesis. Todos nacemos con la capacidad de desarrollar este tipo de inteligencia.

El pensamiento lógico matemático es fundamental para comprender conceptos abstractos, razonamiento y comprensión de relaciones. Todas estas habilidades van mucho más allá de las matemáticas entendidas como tales, los beneficios de este tipo de pensamiento contribuyen a un desarrollo sano en muchos aspectos y consecución de las metas y logros personales, y con ello al éxito personal. La inteligencia lógico matemática contribuye a: • Desarrollo del pensamiento y de la inteligencia. • Capacidad de solucionar problemas en diferentes ámbitos de la vida, formulando hipótesis y estableciendo predicciones. • Fomenta la capacidad de razonar, sobre las metas y la forma de planificar para conseguirlo. • Permite establecer relaciones entre diferentes conceptos y llegar a una comprensión más profunda. • Proporciona orden y sentido a las acciones y/o decisiones.

Una falacia es un razonamiento no válido o incorrecto pero con apariencia de razonamiento correcto. Es un razonamiento engañoso o erróneo (falaz), pero que pretende ser convincente o persuasivo. Todas las falacias son razonamiento que vulneran alguna regla lógica. Así, por ejemplo, se argumenta de una manera falaz cuando en vez de presentar razones adecuadas en contra de la posición que defiende una persona, se la ataca y desacredita: se va contra la persona sin rebatir lo que dice o afirma.

No debemos confundir validez y verdad, como ya hemos visto y las falacias se caracterizan porque algo falla en el razonamiento mismo, es decir, o falla la forma y falla el contenido o significado ---la materia--- de los argumentos supuestamente lógicos o válidos. Así sn algunos casos el problema es la ambigüedad de algunos términos, que nos permitía utilizarlos con dos sentidos distintos en distintas premisas, con lo que al final llegábamos a una conclusión disparatada. Otras veces, en cambio, lo que están mal son las premisas (partimos de premisas falsas que nos parecen verdaderas). Finalmente, hay veces en que lo que está mal es la relación misma entre las premisas (que no es lógica). 

Por tanto, clasificamos las falacias en formales y no formales o materiales.

Las falacias formales

Las falacias formales son argumentaciones en las que la conclusión no se sigue (ni necesaria ni probablemente) de las premisas. La forma misma del razonamiento es incorrecta, por lo que es imposible deducir lo que se dice en la conclusión.

Se dividen en :

• Falacia de ambigüedad.- Contienen frases o palabras que cambian su manera sutil.

Ejemplo: El fin de una cosa, es su perfección, la muerte es el fin de la vida; por lo tanto la muerte es la perfección de la vida.

• Falacia de insuficiencia.- Se encuentran ocultas ideas que no son probadas o son falsas.

Ejemplo: A mi grupo de amigos les encanta el fútbol. A todo el mundo le gusta.

• Falacia de irrelevancia.- Son aquellos argumentos que no tienen evidencias para llegar a una conclusión, es decir son irrelevantes.

Ejemplo: Dices que no debo copiar. Pero mira quién lo dice

Las falacias no formales

Consulta el apartado 2 Falacias no formales que son razonamientos en los cuales lo que aportan las premisas no es adecuado para justificar la conclusión a la que se quiere llegar. Se quiere convencer no aportando buenas razones sino apelando a elementos no pertinentes o, incluso, irracionales. Cuando las premisas son informaciones acertadas, lo son, en todo caso, por una conclusión diferente a la que se pretende.

Entre los  elementos que posee una falacia informal tenemos:

• Apelación a los sentimientos.- Tratan de manipular y convencer a las personas.

Ejemplo: Si repruebo el examen, mi mamá morirá de tristeza.

• Referencia insuficiente.- Nos trata de convencer pero no puede porque le falta argumentos para poder ser creíble.

Ejemplo: Que de cada cinco personas una nazca en China, no significa que todos aquellos que tienen cinco hijos tienen uno que es chino.

• Conclusión irrelevante.- Son las que no tienen evidencias y ni tampoco importancia.

Ejemplo: Pablo es un buen deportista y debe ganar la copa. Después de todo es un buen tipo, ha donado mucho dinero y es un miembro de un grupo musical.

• Causa falsa.- Son razones falsas que no tienen argumentos.

Ejemplo: El cáncer del pulmón se presenta en personas que fuman cigarrillos, por lo tanto fumar cigarrillos es la causa de este cáncer.